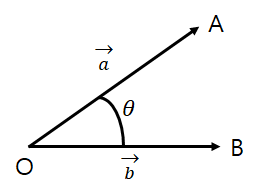
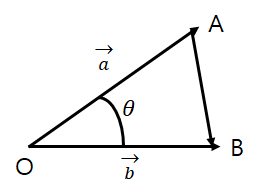
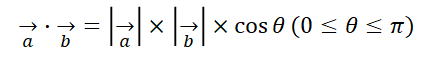벡터의 외적이란?
서로다른 두 벡터 각각에 수직인 방향벡터를 만드는 것.

외적의 특징
1. 벡터 A와 B의 외적 A X B는 벡터 A와 수직이고, B와도 수직이다.
2. 내적과 달리 교환 법칙이 성립되지 않으며, 순서를 바꾸면 반대 방향의 벡터가 나온다. A X B = -(A X B)
3. 내적과 동일하게 분배 법칙은 성립한다. A X ( B + C ) = ( A X B ) + ( A X C )
4. 외적의 벡터의 크기는 평행사변형의 넓이 이다.
5. 두 벡터가 평행하면 크기는 0이다. sin0의 값이 0이기 때문이다.
왼쪽 오른쪽 판별하기

월드 공간의 UP 방향 벡터를 U, 플레이어의 Forward 방향을 F, 플레이어에서 물체를 가르키는 방향을 A라고 했을 때, 벡터 F와 벡터 A를 외적한다. 이 외적한 벡터를 월드 벡터와 내적을 하였을 때, 양수이면 오른쪽 음수이면 왼쪽에 존재하게 된다.
'게임 수학' 카테고리의 다른 글
| 투영 행렬 유도하기 (0) | 2019.12.17 |
|---|---|
| 백페이스 컬링 (0) | 2019.12.17 |
| 내적을 사용한 시야 판별 (0) | 2019.12.17 |
| 평면의 방정식과 평면의 공간적 해석 (0) | 2019.12.17 |
| 투영 벡터 공식 유도 (0) | 2019.12.17 |