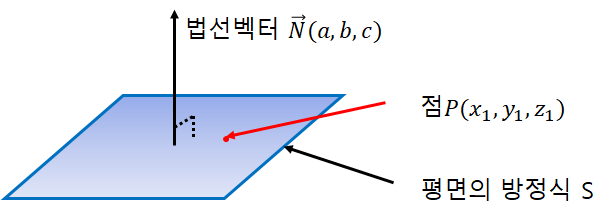
-평면의 방정식
3차원에서 평면은 평면의 방정식으로 해석이 가능하다. 위의 그림의 평면 S는 다음과 같은 식으로 정의할 수 있다.

평면의 방정식을 다시 일반화하면 다음과 같이 정의 할 수 있다.

즉, a,b,c는 평면 안에 속해 있는 임의의 세 점을 선분으로 이은 두 벡터의 외적을 구한 후, 그 외적으로 부터 도출된 벡터의 세 성분이 되며, d는 두 백터의 내적으로 구할 수 있다.
-평면의 공간적 해석
1) a,b 는 0이 아니고 c = 0 일때, z 축에 평행한 평면이 된다.
2) b,c 는 0이 아니고 a = 0 일때, x 축에 평행한 평면이 된다.
3) a,c 는 0이 아니고 a = 0 일때, y 축에 평행한 평면이 된다.
4) a는 0이 아니고 b=c=0 일때, yz 평면에 평행한 평면이 된다.
5) b는 0이 아니고 a=c=0 일때, zx 평면에 평행한 평면이 된다.
6) c는 0이 아니고 a=b=0 일때, xy 평면에 평행한 평면이 된다.
이 때, d값은 특수한 상황일 때, 특수한 성질을 띄게 된다.

이 경우, H는 평면상의 점이 되며, 법선벡터 N과 같은 방향 벡터가 된다. 즉, 이 값은 다음과 같다.

이 값을 평면의 방정식에 대입하게되면, d의 값은 벡터OH의 크기의 절댓값과 같게된다.
즉, 평면의 방정식에서 d의 의미는 평면에서 원점까지의 최단거리를 의미하게 된다.
'게임 수학' 카테고리의 다른 글
| 벡터 내적과 외적을 응용한 왼쪽과 오른쪽의 판별 (0) | 2019.12.17 |
|---|---|
| 내적을 사용한 시야 판별 (0) | 2019.12.17 |
| 투영 벡터 공식 유도 (0) | 2019.12.17 |
| 벡터 내적 공식 유도 : a * b = |a||b|cosθ 유도하기 (0) | 2019.12.17 |
| 선형 변환과 행렬의 관계 (0) | 2019.12.17 |